微积分基本定理怎么理解（微积分基本定理介绍)

微积分基本定理

这个定理的证明，有一定的难度。我特地重新看了大学微积分教材，感觉自己绝对没有能力背着书推导一遍。这其中的原因当然首先要怪自己水平太烂，但是也足以说明这个证明的难度。

那么有没有更好的证明方法呢？可能没有——因为如果有更好的方法那早就进入教材了。但是，我们总可以找到一个更好的理解方法。这个更好的理解方法就是借助运动学的速度和位移（严格说是位置坐标）概念。

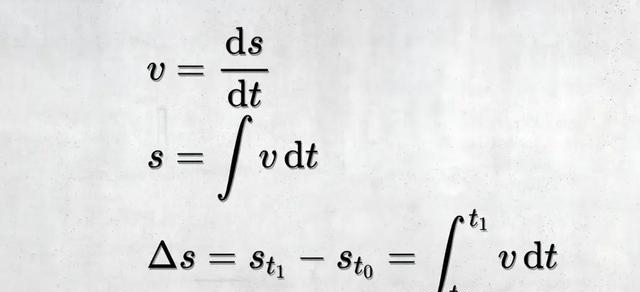
我们知道，速度就是位置坐标随时间的变化率，即速度是位置坐标（函数值）对时间（自变量）的导数。那么显然的，在已知速度函数即导函数的情况下，反过来求位置坐标函数就是求导过程的逆运算。当然说到细节的话应该是得到一系列彼此相差一个常数的函数。这就是不定积分的物理意义。

既然求位置坐标是不定积分，而计算一段时间内的位移也就是定积分，当然是两个时间点之间的位置变化，也就是原函数在两个时间点之间的差值。这还不好理解吗？

我认为，用导数和积分的物理意义来理解微积分基本定理，比传统的用其几何意义（切线斜率和面积）更方便理解。因为说实话，切线和面积的关系不太明显。

很可能有人会这样批评：我们只能用数学证明物理定理，不能反向而行，因为数学可以是物理的工具，物理绝不可能是数学的工具。但是我前面一开始就说过，这不是严格的证明，只是希望帮助大家理解。这里说的理解，其实就是希望大家“从心眼里认同”，这样才能保证不会出错。不然就会像“是人”“斯人”的官司一样，尽管一方拿出了无数证据，另一方还是觉得自己有理。由此可见，在学习数学的过程中，适当联系其它学科，特别是联系到这些数学问题的实际意义，很可能会更好地加深对数学的理解。