时间:2022-12-27 07:40
互相垂直的两条直线的交点称为垂足
提要
在已经学习了直线,射线,线段和角的有关知识的基础上,进一步研究平面内两条直线相交形成4个角的位置和数量关系,为今后学习几何奠定了基础,同时也为证明几何题提供了示范作用。要注意“垂直”是两条直线相交的特殊情形,要注意“垂线段最短”这一性质的理解和正确运用。
知识全解
一.对顶角
(1)概念:一个角的两边是另一个角的两边的方向延长线,这样的两个角是对顶角。
(2)性质:对顶角相等。
二.垂直的定义
如果两条直线相交成直角,那么这两条直线互相垂直,如图所示
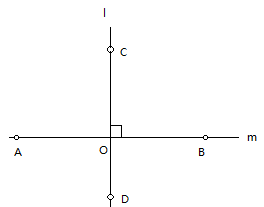
直线AB,CD相交于点O,∠BOC=90度,此时说直线AB与CD互相垂直,记作AB⊥CD。其中AB所示CD的垂线,CD也称为AB的垂线。互相垂直的两条直线的交点称为垂足(如图中的点O)。
提示:(1)在垂直的定义中要强调只有一个角是直角即可。不必说四个角都是直角,因为其他三个直角都可推导出来。
(2)两条直线互相垂直,是指两条直线而言。因此,说到垂线,一定是两条直线的位置关系。
三.垂线的画法
过一点作已知直线的垂线的画法有两种情况:一是过直线上一点画已知直线的垂线;二是过直线外一点画已知直线的垂线。一般用三角板或量角器画图。用三角板画图要注意“一贴”,即贴住已知直线,“一靠”,即靠住已知点再画线。
提示:画线段或射线的垂线就是画它们所在的直线的垂线,线段的垂足有时在延长线上,有时在反向延长线上。
四.正确理解垂线的性质
性质1:过一点有且只有一条直线与已知直线垂直。
注意:(1)“有且只有”中,“有”指“存在”,“只有”指“唯一”。
(2)“过一点”的点在直线外,或在直线上都可以。
性质2:直线外一点与直线上各点连接的所有线段中,垂线段最短,简称垂线段最短。
提示:直线外一点或直线上各点的连线段有无数条,但垂线段只有一条,如图所示
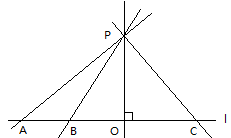
设P是直线l外一点,PO⊥l,垂足为O,线段PO称为点P到直线l的垂线段。由性质1可知,这样的垂线段有一条,垂足也只有一个,故垂线段唯一,而直线l上除O点外的其他各点与P的连接线段称为斜线段,通过度量比较,垂线段最短。
方法点拨
类型1 垂直的作图
例1 如图所示
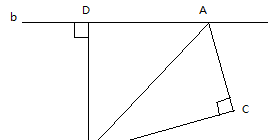
火车站,码头分别位于A,B两点,直线a和b分别表示铁路与河流
(1)从火车站到码头怎样走最近,画图并说明理由
(2)从码头到铁路怎样走最近,画图并说明理由
(3)从火车站到河流怎样走最近,画图并说明理由
【分析】(1)从火车站到码头的距离是点到点的距离,即两点间的距离。依据两点间线段最短解答。
(2)从码头到铁路的距离是点到直线的距离,依据垂线段最短解答
(3)从火车站到河流的距离是点到直线的距离,依据垂线段最短解答。
【解答】(1)沿AB走,两点之间线段最短
(2)沿BD走,垂线段最短
(3)沿AC走,垂线段最短。
【点评】根据具体的问题正确判断出是点到点的距离还是点到直线的距离是解答问题的关键。
类型2 角度的计算
例2 如图所示
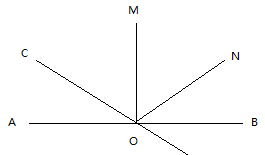
直线AB,CD相交于O,MO⊥AB于O,∠BOC:∠BON=4:1,OM平分∠NOC。求∠MON,∠BOD的度数。
【分析】根据垂直的定义,角平分线的定义得到∠COA=∠NOB,根据题意求出∠BOC=144度,∠AOC=36度,结合图形计算即可。
【解答】∵MO⊥AB
∴∠AOM=∠BOM=90度
∵OM平分∠NOC
∴∠COM=∠NOM
∴∠COA=∠NOB
∵∠BOC:∠BON=4:1
∴∠BOC:∠AOC=4:1
又∠BOC+∠AOC=180度
∴∠BOC=144度,∠AOC=36度
∴∠BOD=∠AOC=36度
∠MON=∠BOM-∠BON=54度
【点评】本题考查的是对顶角,邻补角的概念和性质,掌握对顶角相等,邻补角之和等于180度是解题的关键。